Intro

「公鑰密碼學」，又稱為「非對稱密碼學」，使用兩個不同的金鑰：一個公鑰和一個私鑰。公鑰用於加密訊息，私鑰用於解密訊息。公鑰是公開的，而私鑰則需保密。其主要應用包括：加密/解密（確保保密性）、數位簽章（提供身份驗證）、金鑰交換（用於會話金鑰）。

PS: 密碼學的關鍵在於達到四個核心要素：保密性（Confidentiality）、資料完整性（Data Integrity）、身份驗證（Authentication）以及不可否認性（Non-repudiation）。

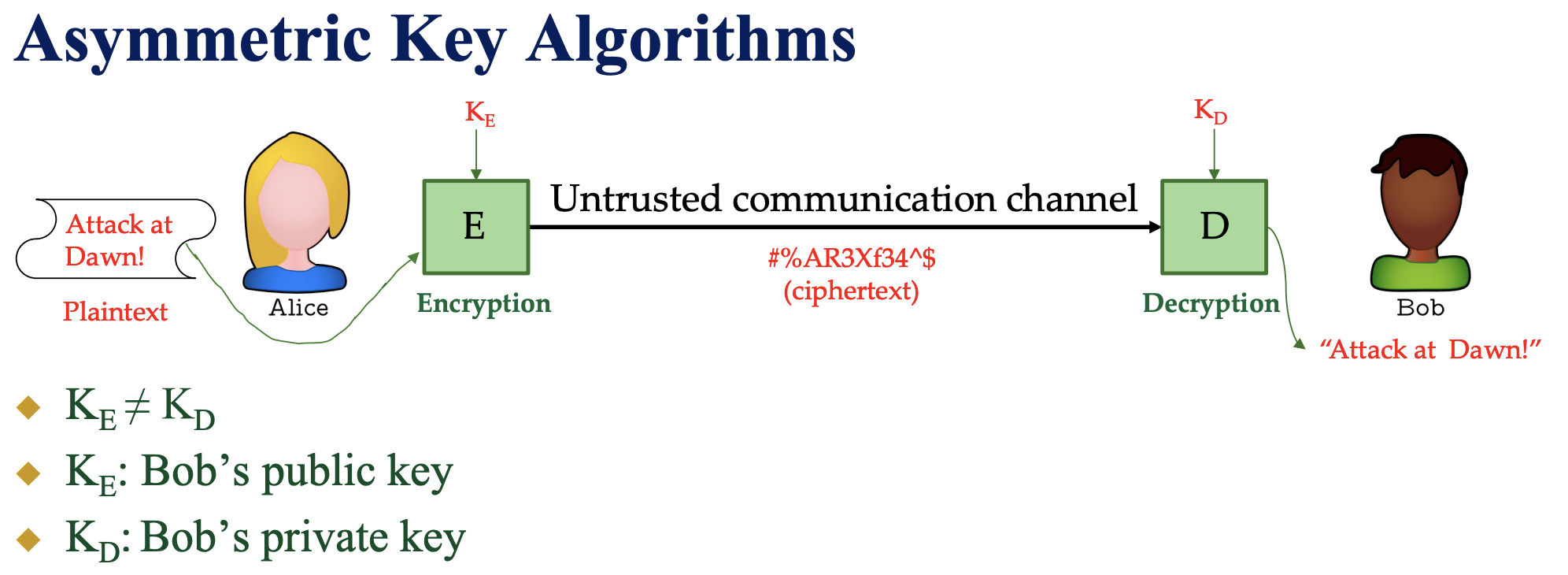
與之相對的“對稱密碼學”中，加密和解密訊息則使用相同的密鑰。

核心構造：陷門單向函數

在“公鑰密碼學”中，加密訊息的公鑰是公開的，而我們需要設計一種結構，使得訊息解謎對持有私鑰的人是簡單的，而對沒有私鑰的人是極其困難——不可解的。

這裏的核心思想也就是構造一個Trapdoor One Way Function 陷门单向函数，即：

Trapdoor One Way Function 陷门单向函数

1. 单向性（One-way）：函数 f(x) = y 在正向计算非常容易，但给定 y 想要找到 x 使得 f(x) = y 在计算上是困难的。
2. 陷门（Trapdoor）：存在一个特殊的秘密信息（陷门），如果知道这个秘密，就能够高效地计算反向函数，即从 y 求出 x。

傳統數論的兩類陷門單向函數

1. 大質數分解問題 Factorization of two primes

Given P, Q are two primes and N = P*Q
It is easy to compute N
However given N it is difficult to factorize into P and Q

用於RSA加密體系

2. 離散對數問題 Discrete Log Problem

Consider b and g are elements in a finite group and bk=g, for some k
Given b and k it is easy to compute g
Given b and g it is difficult to determine k

用於Diffie-Hellman加密體系以及變體ECC橢圓曲線加密體系

RSA Cryptosystem

基於大質數分解問題，RSA系統包含以下步驟：

密鑰生成步驟：

1. 選擇兩個不同的大質數 p, q
2. 計算模數 n = p × q
3. 計算歐拉函數值 φ(n) = (p - 1)(q - 1)
4. 選擇公鑰指數 b，要求 1 < b < φ(n) 且 gcd(b, φ(n)) = 1
5. 計算私鑰指數 a ≡ b⁻¹ mod φ(n)

結果得到： 公鑰 pk = (n, b) 私鑰 sk = (p, q, a)

這裡的歐拉函數 φ(n) 用於計算在 1 到 n 之間與 n 互質的數的個數。

加密和解密過程：

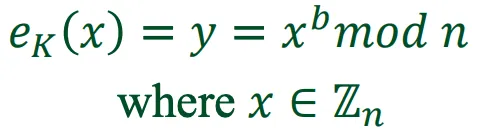
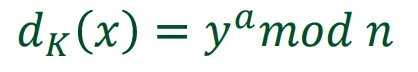
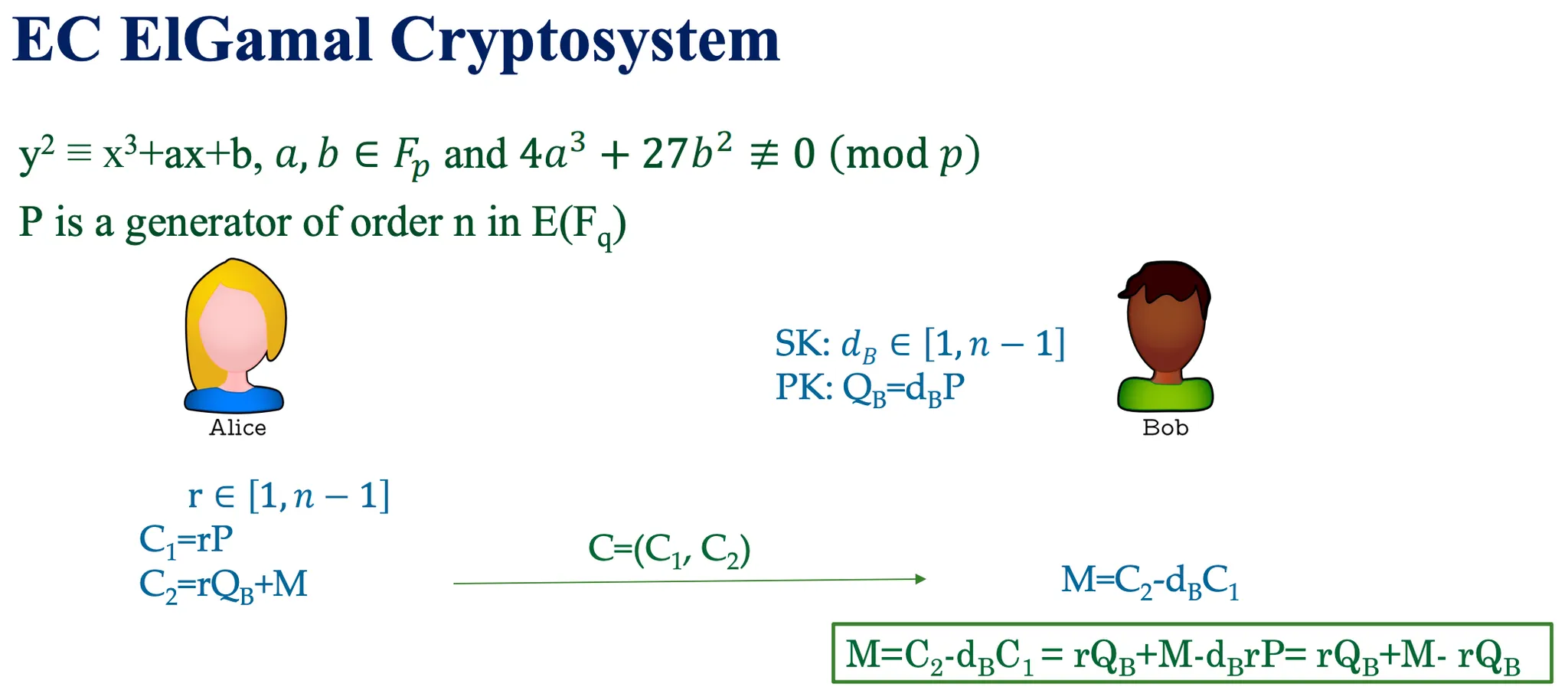
Elgamal Cryptosystem

基於離散對數DLP問題。它的安全性依賴於有限群中計算離散對數的困難性。

• 公鑰：由群元素 g、私鑰 x 和 h = gˣ 組成
• 加密：選擇隨機數 y，將消息 m 加密為 (c₁, c₂) = (gʸ, m·hʸ)
• 解密：利用私鑰 x 計算 m = c₂/c₁ˣ

Elliptic Curve Cryptography (ECC)

屬於DLP離散對數問題的變體。

橢圓曲線的定義（模運算）

解集構成阿貝兒群（Abelian group）

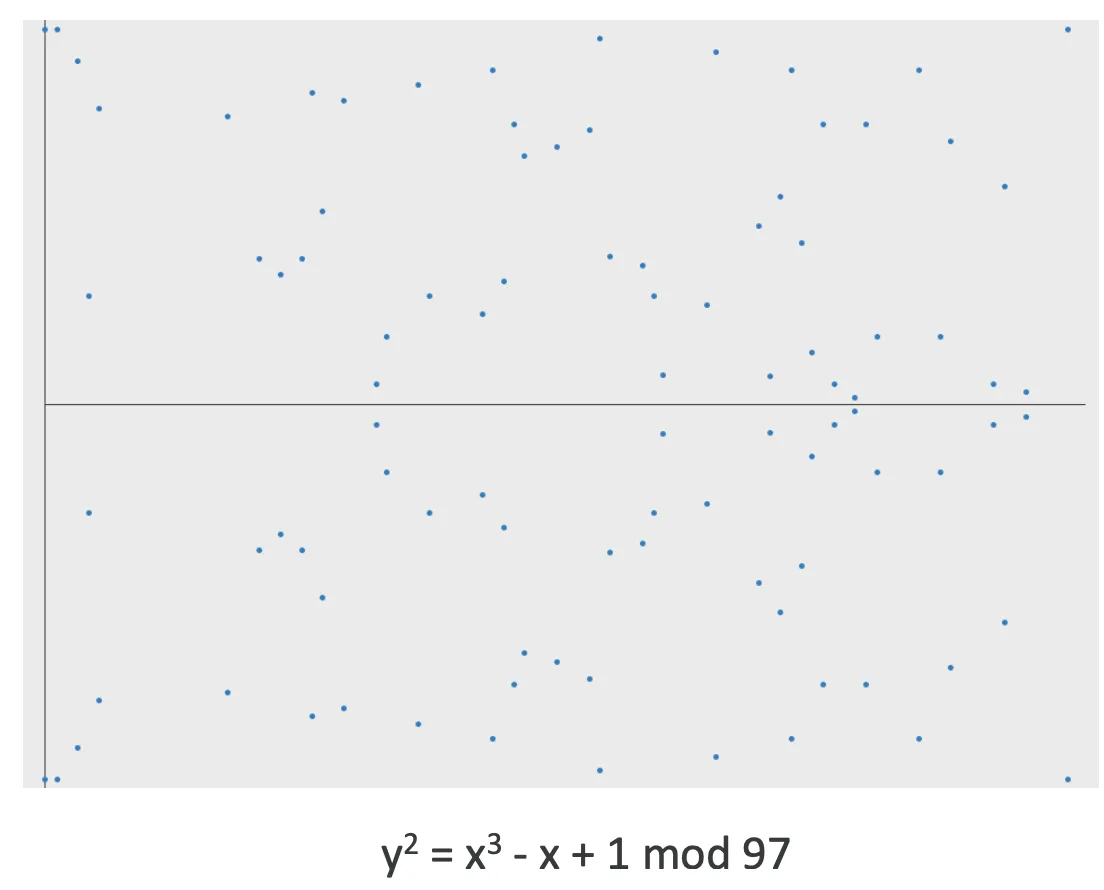
Elliptic Curve Discrete Logarithm Problem (ECDLP)

给定：椭圆曲线 E，基点 P，目标点 Q = kP 求解：整数 k，使得 Q = kP

為什麼在 ECC 中使用有限域？

在實際的密碼系統中，我們選擇在有限域（Finite Field）上定義橢圓曲線，而不是在實數域上，因為

• 計算精確性：有限域使用精確的整數運算，避免實數域的計算誤差。
• 存儲效率：元素可用固定長度比特串表示，提高計算效率。
• 安全性：有限域使離散對數問題更難解決，避免實數域連續性帶來的安全隱患。
• 運算效率：加法、乘法等運算快速，適合實際應用。

通常使用的有限域包括：

• 素數域 GF(p)：其中 p 是一個大質數
• 二元擴展域 GF(2ⁿ)：特別適用於硬件實現

基於傳統數論的公鑰密碼學的侷限

• 量子威脅：Shor量子算法可在多項式時間內破解傳統數論難題
• 密鑰增長：為提升安全強度需要指數級別的密鑰增長，影響效率
• 結構單一：主要依賴於少數幾個數論問題（質因數分解、離散對數）
• 理論瓶頸：缺乏新的可靠數學難題作為密碼學基礎

傳統數論問題的複雜性

• 大質數分解問題 (Integer Factorization)：尚未被證明為 NP 完全問題。在經典計算機上，最佳算法具有次指數時間複雜度，但使用 Shor 量子算法可在多項式時間內解決。
• 離散對數問題 (DLP)：雖非 NP 完全問題，但被視為計算上的困難問題。在經典計算機上需要次指數時間，但同樣可被 Shor 量子算法在多項式時間內解決。
• 橢圓曲線離散對數問題 (ECDLP)：較一般離散對數問題更為困難，目前最佳算法仍需指數時間複雜度。然而，此問題同樣易受量子計算威脅。

格理論的引入

格理論問題的複雜性與應用

• 最短向量問題 (SVP)：在格中尋找最短的非零向量，已被證明在某些範數下是 NP-hard 問題，其近似版本同樣保持困難性。
• 最近向量問題 (CVP)：在給定目標點時尋找最近的格點，這是一個 NP-hard 問題，常用作解密算法的基礎。
• 學習帶誤差問題 (LWE)：解決線性方程組 As + e = b (mod q)，其中已知 A 和 b 求解 s。此問題具有平均情況困難性，且基於最壞情況的格問題，表現出優異的量子抗性。
• 短整數解問題 (SIS)：給定隨機矩陣 A，尋找短向量 x 使得 Ax = 0 (mod q)。此問題與 LWE 相對偶，同樣具有優異的量子抗性和平均情況困難性。

格理論的優勢

相比傳統數論，格理論中的平均情況難度可歸約到最壞情況，提供更強的安全保證。這與傳統密碼學中平均情況歸約到特殊情況的方式形成鮮明對比。同時，格理論提供了豐富的難題（如SVP、CVP、LWE、SIS等），使得密碼方案設計更加靈活多樣。